Nash Equilibrium
定義
- 奈許均衡 (Nash Equilibrium) 是 賽局理論 中的核心概念
- 指在兩人以上的非合作賽局中，若每位參與者皆已知他人策略，且無人能單獨改變自身策略來獲得更大利益，則當前的策略組合即為奈許均衡
- 換言之，當每位參與者都選擇對自己最有利的行動，並預期他人也如此，最終形成相互穩定的選擇組合，即為奈許均衡
- 若有任一方單獨改變策略，其結果對自身無提升，這正是奈許均衡的本質
- 兩名嫌犯各自決定是否招供
- 若皆不招供，將共同獲得最短刑期
- 但因彼此擔憂對方招供導致自己受重罰，最終兩人都選擇招供
- 此決策組合即為奈許均衡
|
乙合作 (沉默) |
乙背叛 (指控) |
| 甲合作 |
各服半年 |
甲判 10 年，乙釋放 |
| 甲背叛 |
甲釋放，乙判 10 年 |
各服 5 年或 15 年 (有不同版本) |
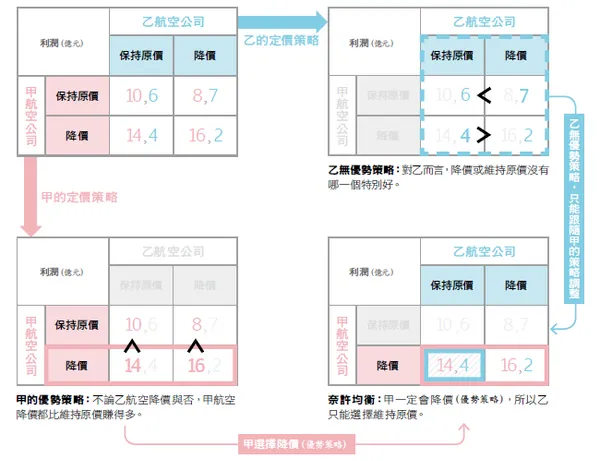
補充例子：航空公司定價賽局
- 有兩家航空公司 (甲與乙)，皆可選擇「保持原價」或「降價」
- 利潤分別依照雙方的價格策略而定，如圖所示
- 若乙保持原價，甲降價可獲更高利潤 (14.4 > 10.6)
- 若乙降價，甲降價仍可獲更高利潤 (16.2 > 8.7)
- 因此，不論乙的選擇為何，甲皆會選擇「降價」為最有利策略 (占優策略)
- 乙同理，無論甲的選擇為何，降價總是帶來較高利潤，因此乙也會選擇「降價」
- 雙方最終都選擇「降價」，此組合 (甲降價，乙降價) 即為奈許均衡，雖非雙方總利潤最大但具穩定性
數學表示
- 若策略組合 ss 滿足對任一參與者 ii 而言，即便其單獨改變策略 (他人策略不變)，收益亦無法提升，則 ss 為奈許均衡
- 表示如下：$$p_i(s) = \max_{r_i}[p_i(s; r_i)]$$
- 為參與者 i 的收益，s 為所有人的策略組合， 為 i 可採的其他行動
應用說明
- 奈許均衡可解釋現實中許多效率不佳但無人改變的情況
- 例子包括價格競爭、薪資停滯、產業慣例等
- 即使所有人皆有改變空間，但只要單方行動無利可圖，現況便會維持奈許均衡
進階變形
- 混合策略奈許均衡：參與者以不同行動的機率做決策，而非僅選擇一種行動
- 子賽局完美均衡與貝氏奈許均衡：適用於具行動順序或資訊不完全的複雜情境